• 中考
• 高考
• 考研
• 公务员
• 自考
• 辅导
• 留学

　　所谓定值问题，是指按照一定条件构成的几何图形，当某些几何元素按一定的规律在确定的范围内变化时，与它有关的元素的量保持不变(或几何元素间的某些几何性质或位置关系不变)。

　　几何定值问题的基本特点是：题设条件中都包含着变动元素和固定元素，变动元素是指可变化运动的元素，固定元素也就是“不变量”，有的是明显的，有的是隐含的，在运动变化中始终没有发生变化的元素，也就是我们要探求的定值。

　　下面给出三个例题：

　　例1：如图，扇形OAB的半径OA=3，圆心角∠AOB=90°.点C是弧AB上异于A，B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E.连接DE，点G，H在线段DE上，且DG=GH=HE.

　　(1)求证：四边形OGCH是平行四边形；

　　(2)当点C在弧(AB上运动时，在CD，CG，DG中，是否存在长度不变的线段？若存在，请求出该线段的长度；

　　(3)求证：CD平方+3CH平方是定值。

　　解题思路：延长OG交CD于N，利用题中的三等分点、平行四边形和三角形中位线的性质，实现把线段ON转化成线段CH的倍分关系，再以Rt△OND为基础，通过勾股定理，使问题得以解决。

　　例2：在平面直角坐标系中，边长为2的正方形OABC的两顶点A，C分别在y轴，x轴的正半轴上，点O在原点，现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转.旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N.

　　(1)求OA在旋转过程中所扫过的面积；

　　(2)旋转过程中，当MN与AC平行时，求正方形OABC旋转度数；

　　(3)设△MBN的周长为P，在正方形OABC旋转的过程中，P值是否有变化？请证明你的结论.

　　解：⑴ ⑵22.5° ⑶P值无变化.

　　理由如下：如图，延长BA交y轴于E点，可证明△OAE≌△OCN，得OE＝ON，AE＝CN，又∠MOE＝∠MON＝45°，OM＝ON，∴△OME≌△OMN，得MN＝ME＝AM＋AE＝AM＋CN.∴P＝MN＋BN＋BM＝AM＋CM＋CN＋BN＋BM＝AB＋AC＝4.

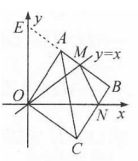
　　例3：如图，已知△ABC为直角三角形，∠ACB=90°，AC=BC，点A，C在x轴上，点B坐标为(3，m)(m＞0)，线段AB与y轴相交于点D，以P(1，0)为顶点的抛物线过点B，D.

　　(1)求点A的坐标(用m表示)

　　(2)求抛物线的解析式；

　　(3)设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F.试证明：FC(AC+EC)为定值.

相关新闻：

中学语文阅读理解的24个满分秘笈

初中语文三年长线规划，让你不惧中考改革

用营养良方疗救学生阅读“亚健康”

背文言文课文背吐了？7个小技巧

名师指导：中考数学选择题精妙解题法